The core concepts of mathematics form the backbone of data science, machine learning, and artificial intelligence for making strategic decisions. As it is said, it is not possible to become an artisan without creativity; similarly, it is not possible to become a connoisseur in these fields without a thorough grasp of mathematics. With the help of mathematics, we can help determine the correct parameter values and validation methods, along with the interval and uncertainty. It is the soul behind designing machine learning algorithms that automatically make predictions from learning data, considering accuracy, the complexity of the model, training time, and the number of features. We will run through some of the essential concepts in this blog post for data scientists, machine learning engineers, and artificial intelligence researchers.
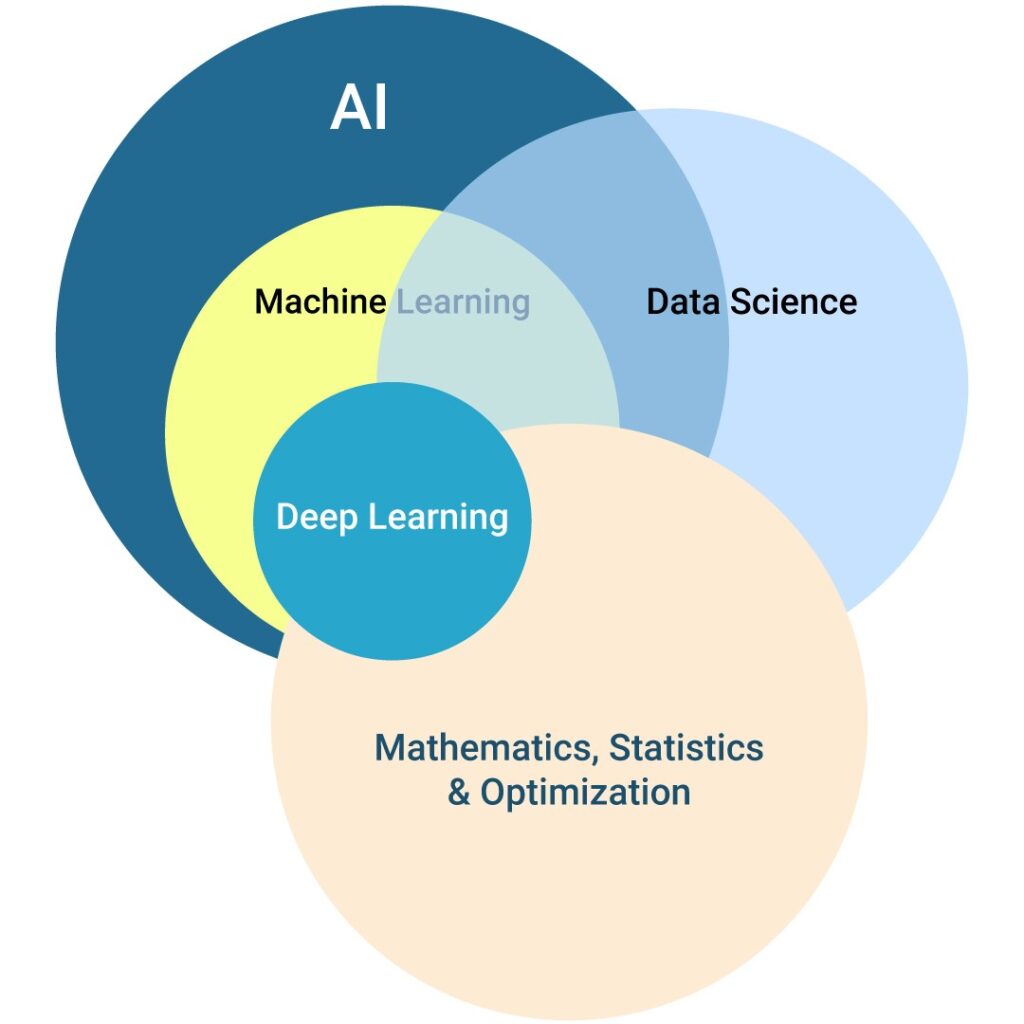
Mathematical Concepts Important for Data Science, Machine Learning, And Artificial Intelligence
After understanding the necessity for math, the next question arises: what standard of math is needed? What notions ought one to understand? The basis of machine learning lies in essential concepts: Linear Algebra, Probability & Statistics, Calculus, Optimization, and Graph Theory. You will encounter them frequently in your Data Science, Artificial Intelligence, and Machine Learning career.
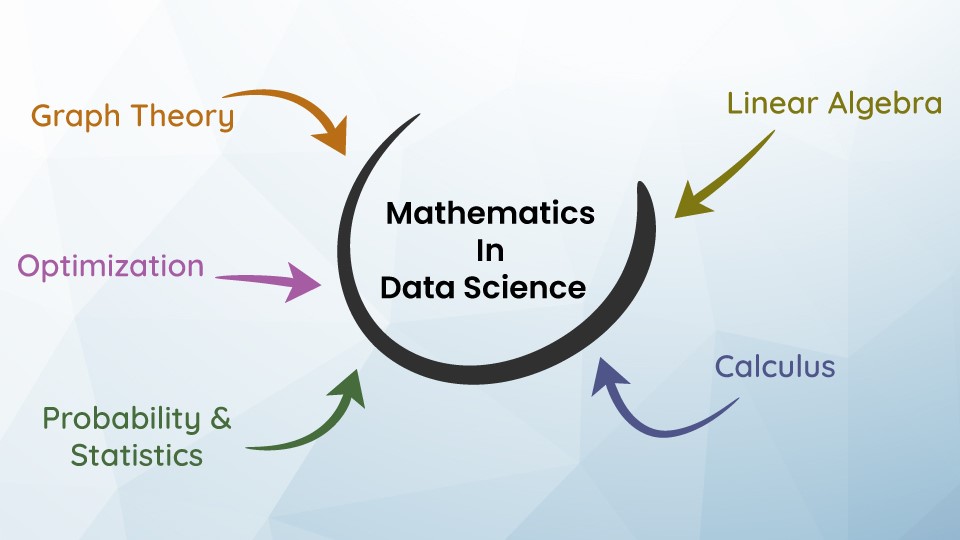
Linear Algebra
An important aspect of linear algebra is the study of linear equations, vectors, and matrices. It is an essential tool for data scientists, as it helps them to manipulate and transform data efficiently. Machine learning algorithms heavily rely on matrix operations and linear algebra concepts like eigenvectors and eigenvalues. These concepts are crucial for techniques like principal component analysis (PCA) used to reduce the dimensionality of data. Linear algebra is also laboriously used in neural networks to process and represent the networks. Understanding linear algebra and its core concepts helps with problem formulation.
Calculus
Without losing generality, every machine learning problem is an optimization problem. Calculus is a branch of mathematics that deals with the study of continuous change. Data scientists use calculus to optimize functions and minimize errors. Multivariate calculus helps machine learning researchers solve optimization problems. Machine learning algorithms like gradient descent, a widely used optimization technique, require an understanding of calculus. Calculus concepts like derivatives and integrals are used to compute gradients and find the minimum or maximum values of functions.
Probability and Statistics
Probability and statistics are essential for data science, machine learning, and artificial intelligence. Probability is the study of random events and their likelihood, while statistics is the science of collecting, analyzing, and interpreting data. Data scientists use probability and statistics to model uncertainty and make predictions. Machine learning algorithms like naive Combinatorics, Axioms, Bayes’ Theorem, Variance & Expectation, Random Variables, Logistic Regression, Conditional, and Joint Distributions use probability theory to make predictions.
Optimization
Optimization is finding the optimum accuracy of some function or model. In data science and machine learning, optimization is used to find the optimal values of parameters for a given model. In order to minimize loss functions and maximize accuracy, techniques like gradient descent and stochastic gradient descent use optimization.
Graph Theory
A graph, in the context of graph theory, is a network of vertices (also called nodes or points) and edges (also called links or lines). Nodes are the entities that hold information, and edges mean connections between nodes that also hold information. Graph theory is essential for artificial intelligence, especially in natural language processing and computer vision. Graph theory is used by techniques of convolutional neural networks (CNNs) and recurrent neural networks (RNNs) to model data and make predictions.
Aside from the mentioned concepts, math level also depends on an individual’s interest and research topic. In conclusion, a sound understanding of mathematical concepts is essential for anyone working with data science, machine learning, or artificial intelligence. Linear algebra, calculus, probability and statistics, optimization, and graph theory are just a few of the critical mathematical concepts that every data scientist, machine learning engineer, and artificial intelligence researcher should master.